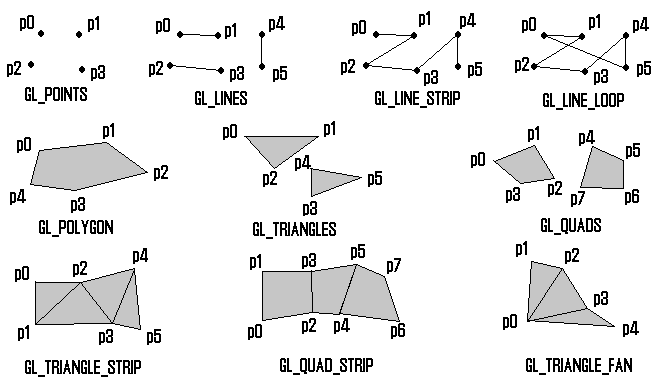
Kuva 3.1. Geometriset mallit.





OpenGL sisältää piirtorutiinit tavallisimmille kaksi- ja kolmiulotteisille geometrisille kappaleille. Näitä ovat pisteet, viivat, kaaret, neliöt, ympyrät, pallot, kuutiot, kartiot ja sylinterit. Haluttaessa piirtää jokin edellisistä poikkeava objekti, on se koottava niistä.
Geometristen objektien piirto tapahtuu aina kutsujen glBegin (GLenum mode) ja glEnd ( ) välissä. Kontrollipisteet annetaan aliohjelmakutsulla glVertex{234}{s i f d}v( ). Piirrettävä objekti määritellään glBegin(GLenum mode)-kutsulle välitettävällä parametrilla mode. Sen on oltava jokin seuraavista (katso Kuva 3.1.):

Aliohjelmakutsujen glBegin(GLenum mode) ja glEnd( ) välissä sallitut OpenGL:n omat aliohjelmakutsut on rajattu tarkasti (katso OpenGL Programming Guide s.38). Kontrollipisteiden määrittelyn lisäksi siellä saa olla vain objektin väriin, materiaaliin ja reunoihin liittyviä aliohjelmakutsuja. Ohjelmointikielen omia funktioita ja laskusuorituksia koodin seassa saa olla vapaasti. Ympyrän kaaren approksimaatio voitaisiin määritellä esimerkiksi näin:
Pisteet esitetään kolmiulotteisessa koordinaatistossa aina neljän reaaliluvun (x,y,z,w) avulla. Mikäli pisteen paikan määräämiseksi riittää kaksiulotteinen koordinaatisto, voidaan kaksi viimeistä lukua jättää määrittelemättä ja OpenGL oletuksena antaa z-koordinaatille arvon 0.0 ja w-koordinaatille arvon 1.0. Jos neljäs reaaliluku w määritellään erisuureksi kuin nolla, kolme ensimmäistä koordinaattipistettä jaetaan sillä (x/w, y/w, z/w). Oletuksena w:n arvo on 1.0.
Useimmiten piste esitetään yhden pikselin kokoiseksi, joka on myös oletuksena OpenGL:ssä. Mikäli piste halutaan suuremmaksi kuin pikseli, voidaan sen koko määritellä kutsulla glPointSize(GLfloat size). Esimerkiksi parametrin size arvolla 2.0 pisteen koko on 2x2 pikseliä.
Viivojen piirrossa annetaan aina viivan alku- ja loppupiste, jotka yhdistetään viivaksi. Oletuksena viivojen paksuus on yksi pikseli ja tyyli on normaali jatkuva viiva. Viivan paksuus voidaan muuttaa kutsulla glLineWidth(GLfloat width).
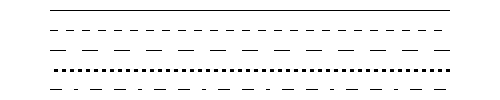
Lisäksi viivatyyppi voidaan valita katkoviivaksi, pisteviivaksi tai näiden yhdistelmäksi. Viivan tyyli määritellään kutsulla glLineStipple (GLint factor, GLshort pattern). Toinen parametri pattern on 16-bittinen sarja nollia ja ykkösiä. Ykkösellä piirretään viivaa ja nollalla piirtoa ei tapahdu. Ensimmäinen parametri factor venyttää yhden bitin vaikutusaluetta. Jos se on ykkönen, jokainen bitti vaikuttaa yhteen pikseliin. Jos factor on kakkonen, jokainen bitti vaikuttaa kahteen pikseliin jne. Sallittu arvo ensimmäiselle parametrille on kokonaisluku välillä 1-255. Katkoviivan piirto on tehtävä vielä mahdolliseksi kutsulla glEnable (GL_LINE_STIPPLE).
Kuvassa 3.2. olevien eri viivatyyppien piirtoon vaadittavat aliohjelmat on esitetty seuraavassa:
{
glColor3f( 0.0, 0.0, 0.0 ); // Piirtoväri mustaksi. |
Polygonit koostuvat useammasta viivasta. Viimeisen viivan loppupiste palaa aina ensimmäisen viivan alkupisteeseen. Polygonit voivat käytännössä olla erittäin monimutkaisia. OpenGL onkin joutunut rajoittamaan polygonien määrittelyä aika rajusti:
Syy rajoituksiin polygonien esityksessä löytyy tietenkin nopeuden maksimoinnista. Yksinkertaisen ja konveksin polygonin "täyttö" on huomattavasti nopeampaa. Piirrettäessä rautalankamallia, ei rajoituksista siten tarvitse välittää. Usein halutaan kuitenkin piirtää polygoni, joka ei ole yksinkertainen tai konveksi. Miten ongelma ratkaistaan? Kaikki polygonit voidaan paloitella yksinkertaisiksi konvekseiksi polygoneiksi ja esittää siten alkuperäinen polygoni useamman polygonin avulla. OpenGL Utility Library (Luku 8.) sisältää monia valmiita aliohjelmakutsuja monimutkaisempien polygonien esittämistä varten.
Polygonin pinnan määrittelyyn löytyy useita vaihtoehtoja. Sisä- ja ulkopinnat voidaan värittää eri väreillä sekä pinnoille voidaan liittää bittikartta tai kuva.
Polygonien suunnittelussa on syytä huomioida muutama tärkeä yksityiskohta. Kontrollipisteiden suunta (myötä- tai vastapäivään) tulee olla sama kaikilla saman objektin polygoneilla. Toinen huomioitava asia koskee polygonien jakoa useammaksi polygoniksi. Mikäli alkuperäinen polygoni ei ole kolmikulmio, on syytä varmistua, että uusien polygonien kaikki kontrollipisteet sijaitsevat samalla tasolla.
Nelikulmiot ovat erittäin yleisiä graafisissa sovelluksissa. Vaikka nelikulmiot on helppo määritellä polygonin avulla, on niille haluttu määritellä oma aliohjelmakutsu glRect{s i f d}v(TYPE x1, TYPE y1, TYPE x2, TYPE y2). Kutsu määrittelee vasemman alakulman ja oikean yläkulman koordinaattipisteet.
Kaaren piirto voidaan suorittaa kahdella eri tavalla. Mikäli kaarella sijaitsevien pisteiden paikat on helppo laskea, voidaan (ja kannattaa) kaari approksimoida näiden pisteiden avulla. Kaksi peräkkäistä pistettä yksinkertaisesti yhdistetään viivaksi. Tällä tavalla saadaan usein tarpeeksi tarkka approksimaatio kaarelle ja piirto on nopeampi kuin varsinaisen kaaren määrittelyllä piirretty kaari. Kolmiulotteinen pintakin on mahdollista määritellä useamman kolmion yhdistelmänä. Pintoja kuitenkin harvemmin approksimoidaan kolmioiden avulla, koska kolmioiden kontrollipisteiden paikan laskeminen ei ole niin helppoa, eikä niistä muodostuva approksimaatio ole tarpeeksi hyvä.
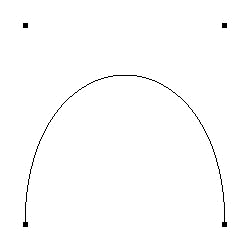
Monet kaaret ja kolmiulotteiset pinnat on kuitenkin mahdollista määritellä matemaattisesti muutamien kontrollipisteiden avulla. Eriasteiset splinefunktiot, kuten B-splinet, NURBS-pinnat (Non-Uniform Rational B-spline), Bézier-kaaret ja -pinnat (katso Kuva 3.3.) sekä Hermite-splinet ovat kaikki käytettävissä, kun halutaan määritellä kaaria tai pintoja.
Kaarien ja kolmiulotteisten pintojen määrittely voi tuntua välillä aika monimutkaiselta. Samalla aliohjelmalla voidaan valita kaaren tai pinnan kohdealueeksi normaali koordinaatisto, värikartta tai kuva. Yksinkertaistettuna niiden määrittely ja piirto toimii seuraavasti:
Yksiulotteisen kaaren piirtoon tarvittavan "kartan" pisteet määritellään aliohjelmalla glMap1{f d}v(GLenum target, TYPE u1, TYPE u2,GLint stride, GLint order, const TYPE* points). Ensimmäinen parametri kertoo kohdealueen. Kaksi seuraavaa lukua määrittelevät välin, jolla parametrin u arvot ovat. Myöhemmin kun "karttaa" piirretään, annetaan aliohjelmalle arvoja, jotka ovat näiden kahden luvun väliltä. Parametri stride kertoo, kuinka monta lukua määrittelee yhden kontrollipisteen. Kontrollipisteiden määrä voi vaihdella, riippuen piirretäänkö tavalliseen koordinaatistoon, värikarttaan vaiko kuvaan. Parametrin order tulisi aina olla yhtä suuri kuin kontrollipisteiden lukumäärä. Osoitin ensimmäisen kontrollipisteen ensimmäiseen koordinaattiin tuodaan viimeisenä parametrina.
Jotta kaari tulee piirrettyä, on kutsuttava aliohjelmaa glEvalCoord1{f d}{v}(TYPE u) useilla u:n arvoilla, jotka ovat "kartan" määrittelyalueen sisällä. Jos esimerkiksi aliohjelmalle glMap1f(..) vietäisiin u1 = 0.0 ja u2 = 1.0, tulisi aliohjelmaa glEvalCoord1f(...) kutsua peräkkäin esimerkiksi arvoilla 0/r, 1/r, 2/r,..., r/r. Parametri r voidaan valita siten, että haluttu tarkkuus saavutetaan.
Kuvassa 3.3. olevan kaaren piirtoon vaadittavat aliohjelmat on esitetty seuraavissa kolmessa koodilaatikossa.
{ } |
GLfloat kontrollipisteet[PISTEITA][3] = { {-4.0,-4.0, 0.0},{-4.0,4.0,0.0}, {4.0,4.0,0.0}, {4.0,-4.0,0.0}}; static void CALLBACK Piirra( ) { } |
Samaan tyyliin määritellään kaksiulotteisen kaaren "kartta". Aliohjelmalle glMap2{f d}(GLenum target, TYPE u1, TYPE u2, GLint ustride, GLint uorder, TYPE v1, TYPE v2, GLint vstride, GLint vorder, TYPE points) tarvitsee kertoa nyt u-suunnassa olevien kontrollipisteiden lisäksi myös v-suunnassa olevat pisteet. Lisäksi on annettava molempien pisteiden lukumäärä stride ja aste order. Piirto suoritetaan taas aliohjelmalla glEvalCoord2{f d}{v}(TYPE u, TYPE v), jolle viedään sekä u että v. Esimerkkikoodi Bézier-pinnan piirrosta on liitteessä 1.
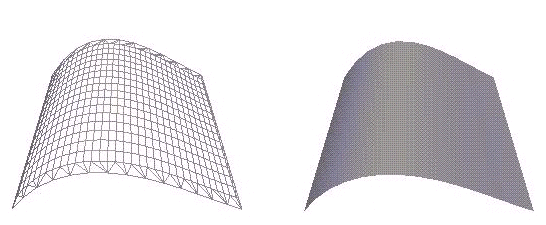
Kolmiulotteiset pinnat määritellään usein NURBS-pintoina. NURBS-pintojen määrittely ei ole sen vaikeampaa kuin edellä esitettävien kaarien määrittelykään. NURBS-pinnat määritellään samalla tavalla kontrollipisteiden, niiden lukumäärän ja asteen mukaan. Lisäksi NURBS-pinnoille kerrotaan, halutaanko käyttää pintamallia vai rautalankamallia.
Kuvan 3.4. NURBS-pintojen piirtoon vaadittavat aliohjelmat on esitetty seuraavissa neljässä koodilaatikossa.
#define UPISTEET 4 GLfloat kontrollipisteet[UPISTEET][VPISTEET][3]; void LaskeKontrolliPisteet( void ) {
for( u = 0; u < UPISTEET; u++ ){
kontrollipisteet[u][v][1] = 2.0*( v - 1.5 ); if( u == 0 )
|
{
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT ); glPushMatrix( ); glRotatef( 45.0, -1.0,0.0,0.0 ); glScalef ( 0.5, 0.5, 0.5 ); gluBeginSurface( theNurb ); gluNurbsSurface( theNurb,
8, knots, 4 * 3, 3, &kontrollipisteet[0][0][0], 4, 4, GL_MAP2_VERTEX_3 ); glPopMatrix( ); glFlush( ); |
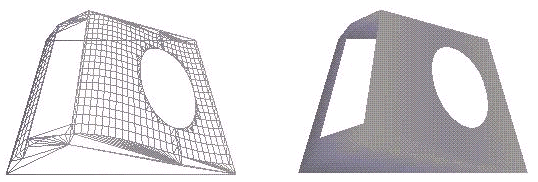
NURBS-pinnan hyvä puoli on lisäksi se, että niille on helppo määritellä reikiä. Jos alue rajataan vastapäivään, täytetään sisäpinta. Kun taas alue rajataan myötäpäivään, tulee siihen reikä (katso Kuva 3.5.).
Kuvan 3.5. reiällisten NURBS-pintojen piirtoon vaadittavat aliohjelmat ovat aliohjelmaa Piirra(void) lukuunottamatta samanlaiset kuin edellä.
{
// Ulkoreuna rajataan vastapäivään. GLfloat ulkoreuna[5][2] = {{ -1.0, -1.0 }, { 1.0, -1.0 }, { 1.0, 1.0 }, { -1.0, 1.0 }, { -1.0, -1.0 }}; // Neliön muotoinen reikä rajataan myötäpäivään. GLfloat nelioReika[5][2] = {{ -0.8, -0.8 }, { -0.8, 0.8 }, { -0.4, 0.8 }, { -0.4, -0.8 }, { -0.8, -0.8 }}; // Ellipsin muotoinen reikä on tehty kahdesta kaaresta. // Alempi kaari rajataan myötäpäivään. GLfloat alempiKaari[4][2] = {{ 0.2, 0.0 }, { 0.2, 0.8 }, { 0.8, 0.8 }, { 0.8, 0.0 }}; // Ylempi kaari rajataan myötäpäivään. GLfloat ylempiKaari[4][2] = {{ 0.8, 0.0 }, { 0.8, -0.8 }, { 0.2, -0.8 }, { 0.2, 0.0 }}; glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT ); glPushMatrix( ); glRotatef( 45.0, -1.0,0.0,0.0 ); glScalef ( 0.5, 0.5, 0.5 ); gluBeginSurface( theNurb ); gluNurbsSurface( theNurb,
8, knots, 4 * 3, 3, &kontrollipisteet[0][0][0], 4, 4, GL_MAP2_VERTEX_3 ); gluPwlCurve( theNurb, 5, &reuna[0][0], 2,
gluEndTrim( theNurb ); gluBeginTrim( theNurb );
GLU_MAP1_TRIM_2 ); gluBeginTrim( theNurb );
&ylempiKaari[0][0], 4,GLU_MAP1_TRIM_2 ); gluNurbsCurve( theNurb, 8, knots, 2, &alempiKaari[0][0], 4, GLU_MAP1_TRIM_2 ); glPopMatrix( ); glFlush( ); |
Kaarien ja pintojen piirtoa varten kannattaa tutustua kirjan OpenGL Programming Guide lukuun 11.




